Visualizing What Batch Normalization Is and Its Advantages

Introduction

Have you, when conducting deep learning projects, ever encountered a situation where the more layers your neural network has, the slower the training becomes?

If your answer is YES, then congratulations, it's time for you to consider using batch normalization now.

What is Batch Normalization?

As the name suggests, batch normalization is a technique where batched training data, after activation in the current layer and before moving to the next layer, is standardized. Here's how it works:

1. The entire dataset is randomly divided into N batches without replacement, each with a mini_batch size, for the training.
2. For the i-th batch, standardize the data distribution within the batch using the formula: (Xi - Xmean) / Xstd.
3. Scale and shift the standardized data with γXi + β to allow the neural network to undo the effects of standardization if needed.

The steps seem simple, don't they? So, what are the advantages of batch normalization?

Advantages of Batch Normalization

Speeds up model convergence

Neural networks commonly adjust parameters using gradient descent. If the cost function is smooth and has only one lowest point, the parameters will converge quickly along the gradient.

But if there's a significant variance in the data distribution across nodes, the cost function becomes less like a pit bottom and more like a valley, making the convergence of the gradient exceptionally slow.

Confused? No worries, let's explain this situation with a visual:

First, prepare a virtual dataset with only two features, where the distribution of features is vastly different, along with a target function:

rng = np.random.default_rng(42)

A = rng.uniform(1, 10, 100)
B = rng.uniform(1, 200, 100)

y = 2*A + 3*B + rng.normal(size=100) * 0.1  # with a little bias

Then, with the help of GPT, we use matplot3d to visualize the gradient descent situation before data standardization:

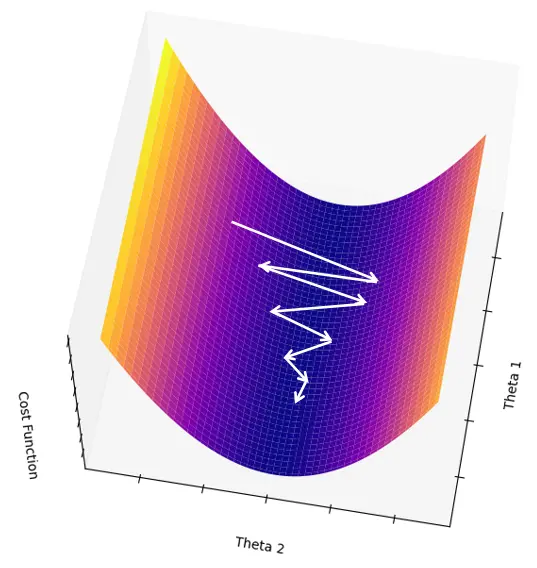
Notice anything? Because one feature's span is too large, the function's gradient is stretched long in the direction of this feature, creating a valley.

Now, for the gradient to reach the bottom of the cost function, it has to go through many more iterations.

But what if we standardize the two features first?

def normalize(X):
    mean = np.mean(X)
    std = np.std(X)
    return (X - mean)/std

A = normalize(A)
B = normalize(B)

Let's look at the cost function after data standardization:

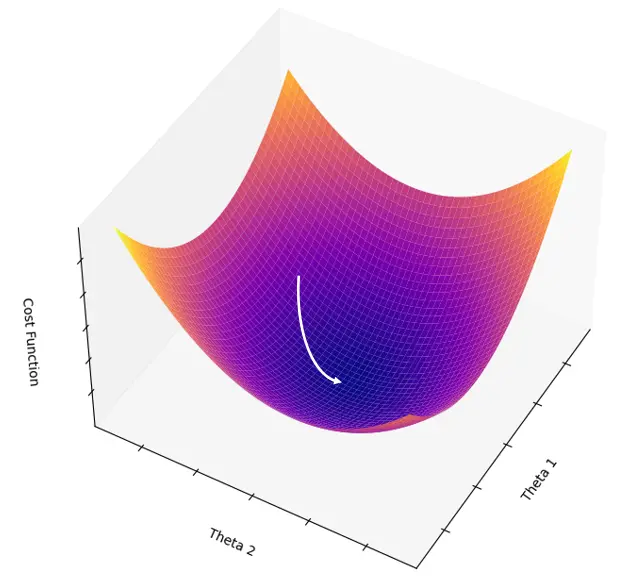
Clearly, the function turns into the shape of a bowl. The gradient simply needs to descend along the slope to reach the bottom. Isn't that much faster?

Slows down the problem of gradient vanishing

The graph we just used has already demonstrated this advantage, but let's take a closer look.

Remember this function?

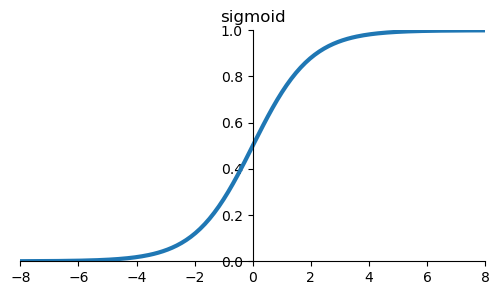
Yes, that's the sigmoid function, which many neural networks use as an activation function.

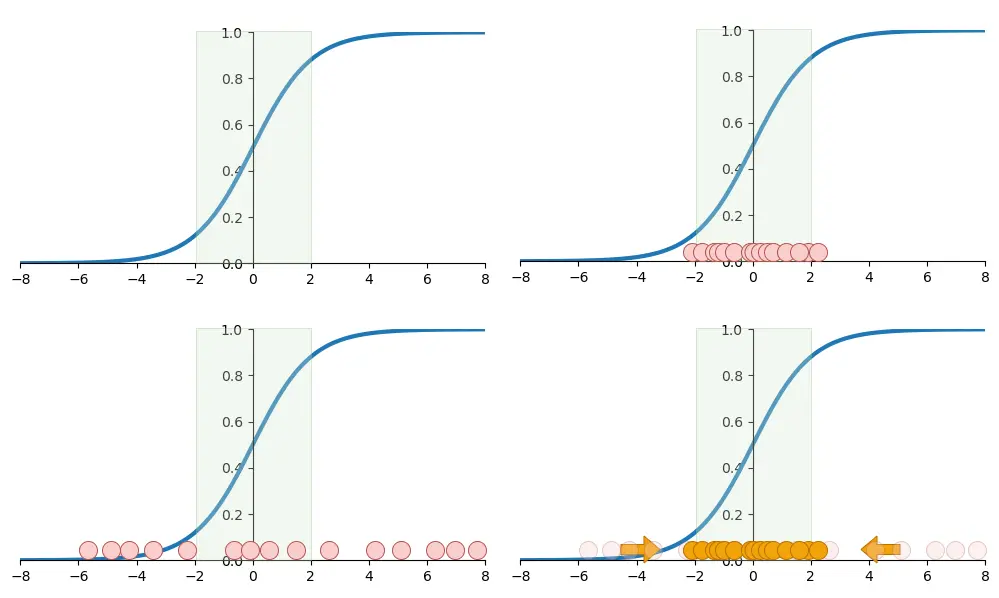
Looking closely at the sigmoid function, we find that the slope is steepest between -2 and 2.

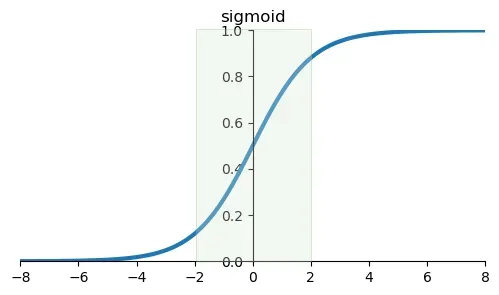
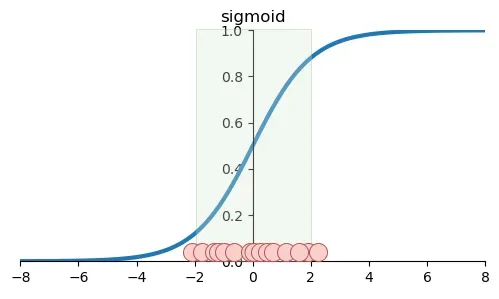
If we reduce the standardized data to a straight line, we'll find that these data are distributed exactly within the steepest slope of the sigmoid. At this point, we can consider the gradient to be descending the fastest.

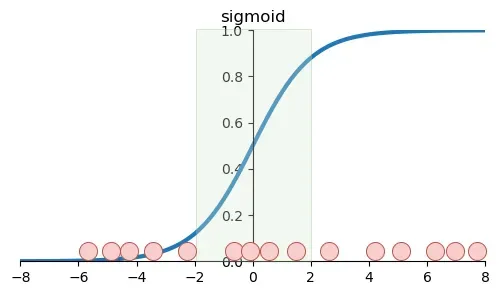
However, as the network goes deeper, the activated data will drift layer by layer (Internal Covariate Shift), and a large amount of data will be distributed away from the zero point, where the slope gradually flattens.

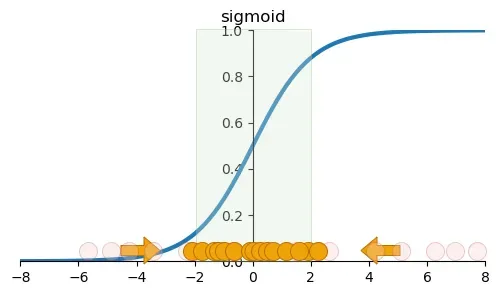
At this point, the gradient descent becomes slower and slower, which is why with more neural network layers, the convergence becomes slower.

If we standardize the data of the mini_batch again after each layer's activation, the data for the current layer will return to the steeper slope area, and the problem of gradient vanishing can be greatly alleviated.

Has a regularizing effect

If we don't batch the training and standardize the entire dataset directly, the data distribution would look like the following:

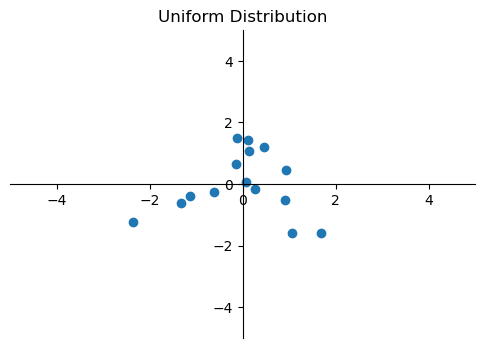
However since we divide the data into several batches and standardize the data according to the distribution within each batch, the data distribution will be slightly different.

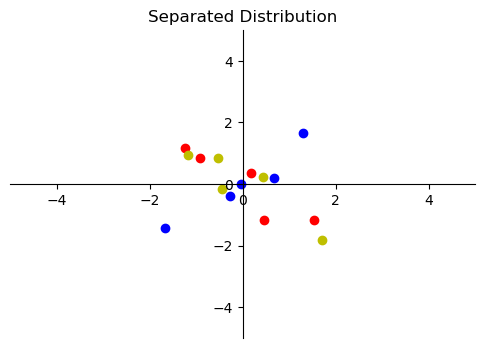
You can see that the data distribution has some minor noise, similar to the noise introduced by Dropout, thus providing a certain level of regularization for the neural network.

Conclusion

Batch normalization is a technique that standardizes the data from different batches to accelerate the training of neural networks. It has the following advantages:

• Speeds up model convergence.
• Slows down the problem of gradient vanishing.
• Has a regularizing effect.

Have you learned something new?

Now it's your turn. What other techniques do you know that optimize neural network performance? Feel free to leave a comment and discuss.